读CSAPP(1) - 信息的表示和处理
计算机存的什么
计算机存储的是二进制,每一位存储的是0或1。大多数计算机使用1字节(也就是8位),作为最小可寻址的内存单位。 每个字节都有一个唯一的数字来标识,也就是地址(address)。每个计算机都有一个字长(word size),也就是常说的64位操作系统,32位操作系统。字长决定了虚拟地址空间的大小, 比如32位有4GB的内存空间,64位则是16EB(1TB = 1024GB,1 EB = 1,024 PB = 1,048,576 TB)。
整数
原码,反码,补码
计算机存储的是二进制,现实中数字有正负之分,二进制如果想表示正负数怎么办呢? 为了解决正负数问题于是有了 原码 ,原码的表示方式是:第一位不再表示有效位,而是符号位,0代表正数,1代表负数
[1001] 这个8位二进制,本该表示 十进制的9,现在他表示为 -1,第一位(1)是符号位,后面的才是真正的值。
| 正数 | 二进制 | 负数 | 二进制 |
|---|---|---|---|
| +0 | 0000 | -0 | 1000 |
| +1 | 0001 | -1 | 1001 |
| +2 | 0010 | -2 | 1010 |
| +3 | 0011 | -3 | 1011 |
| +4 | 0100 | -4 | 1100 |
| +5 | 0101 | -5 | 1101 |
| +6 | 0110 | -6 | 1110 |
| +7 | 0111 | -7 | 1111 |
现在计算机可以存储负数了,我们进行运算操作:
- 十进制:1+1 = 2 ; 二进制则是:0001+0001 = 0010
- 十进制:1 + (-1) = 0;二进制则是:0001+1001 = 1010 结果是-2
1+(-1)时结果会出现问题。 虽然原码表示了正负数,运算却有问题。 为了解决正负数相加问题于是有了反码,反码的表示方式是:在原码的基础上,正数的反码是其本身,负数的反码是符号位不变,有效位取反
| 正数 | 二进制 | 负数 | 二进制 |
|---|---|---|---|
| +0 | 0000 | -0 | 1111 |
| +1 | 0001 | -1 | 1110 |
| +2 | 0010 | -2 | 1101 |
| +3 | 0011 | -3 | 1100 |
| +4 | 0100 | -4 | 1011 |
| +5 | 0101 | -5 | 1010 |
| +6 | 0110 | -6 | 1001 |
| +7 | 0111 | -7 | 1000 |
现在我们看看正负数相加:
- 十进制:1 + (-1) = 0;二进制则是:0001+1110 = 1111 ,正好对应反码表里的 -0
这样就解决了正负数相加的问题,但现在还有一个问题: 0 有两种表示方式:0000和1111,现实中0是不分正负的,计算机也需要解决,否则判断是否为0还需要判断两次(+0和-0)。为了解决0有两种表示类型 于是有了 补码,补码的表示方式是:在反码基础上,正数不变, 负数+1
| 正数 | 二进制 | 负数 | 二进制 |
|---|---|---|---|
| +0 | 0000 | -0 | 0000 |
| +1 | 0001 | -1 | 1111 |
| +2 | 0010 | -2 | 1110 |
| +3 | 0011 | -3 | 1101 |
| +4 | 0100 | -4 | 1100 |
| +5 | 0101 | -5 | 1011 |
| +6 | 0110 | -6 | 1010 |
| +7 | 0111 | -7 | 1001 |
| – | – | -8 | 1000 |
- 原本1111表示-0,+1后: 1111+0001 = 10000,补位后溢出不计入,所以最终结果是0000
- 1000没有人用,于是就给了-8
现在正负0的二进制形式都为0000,并且还多出了一个表示数字-8 再来计算一下正负数相加:
- 十进制:1 + (-1) = 0;二进制则是:0001+1111 = 10000 ,溢出不计入,最终结果0000
运算溢出
如果存储大小为4位,取值范围就是[1000, 0111] -8 ~ 7。
正溢出:
- 十进制:5+5 = 10, 二进制0101+0101 = 1010(十进制结果-6),因为溢出导致将原来符号位的0改成了1,结果变成了负数。
负溢出:
- 十进制-5 + (-5)=-10,二进制1011+1011 = 0110(十进制结果6),溢出位不计入,最终因为溢出导致将原来符号位的1改成了0,结果变成了正数
有符号与无符号的转换
在c语言中整型加上unsigned来表示无符号整数。这样的话补码[1000,01111] 的范围是-8 ~ 7,去掉符号位的话就是[0000,1111] 0~15。
无符号转换成有符号
| 十进制 | 无符号 | 有符号 | 最终十进制结果 |
|---|---|---|---|
| 1 | 0001 | 0001 | 1 |
| 15 | 1111 | 1111 | -1 |
有符号转换成无符号
| 十进制 | 有符号 | 无符号 | 最终十进制结果 |
|---|---|---|---|
| 1 | 0001 | 0001 | 1 |
| -8 | 1000 | 1000 | 8 |
| -1 | 1001 | 1111 | 15 |
扩展与截断数字
扩展(例如从 4位 到 8位)
c语言中short转换为int的操作,小字节转换到大字节,不会对原数据造成丢失
- 无符号数:加 0
| 转换前的十进制 | 4位 | 8位 | 转换后的十进制 |
|---|---|---|---|
| 1 | 0001 | 0000,0001 | 1 |
| 15 | 1111 | 0000,1111 | 15 |
- 有符号数:加符号位
| 转换前的十进制 | 4位 | 8位 | 转换后的十进制 |
|---|---|---|---|
| -1 | 1001 | 1111,0001 | -1 |
| -8 | 1000 | 1111,1000 | -8 |
截取:
如果将w位转为k位,其中w>k,则取后k位,移除 高位 w ~ k 的位。例如 8位 到 4位:则移除前4位,保留后4位。所以可能会丢失高位的数据,导致结果有问题
- 无符号数:直接保留后四位
| 转换前的十进制 | 8位 | 4位 | 转换后的十进制 |
|---|---|---|---|
| 17 | 0001,0001 | 0001 | 1 |
| 255 | 1111,1111 | 1111 | 15 |
- 有符号数:保留后四位,第一位表示符号位(结果是补码)
| 转换前的十进制 | 8位 | 4位 | 转换后的十进制 |
|---|---|---|---|
| -9 | 1000,1001 | 1001 | -7 |
| -15 | 1000,1111 | 1111 | -1 |
浮点数的表示
浮点数在二进制中的存储方式
十进制中 +100.05 可以用科学计数法表示成 +1.0005*$10^2$。这样的话我们就可以根据科学计数法,在二进制中存储了。
将位分成三份存储上面 的值:符号位(0),整数位(10005),阶数位(2)。最后因为是二进制,计算的时候把$10^n$改成$2^n$。
根据国际标准IEEE 754,任意一个二进制浮点数V可以表示成下面的形式:
V=$(−1)^s$𝑀$2^E$
- $(-1)^s$表示符号位,当s=0,V为正数;当s=1,V为负数。
- M表示有效数字,大于等于1,小于2。
- E表示指数位
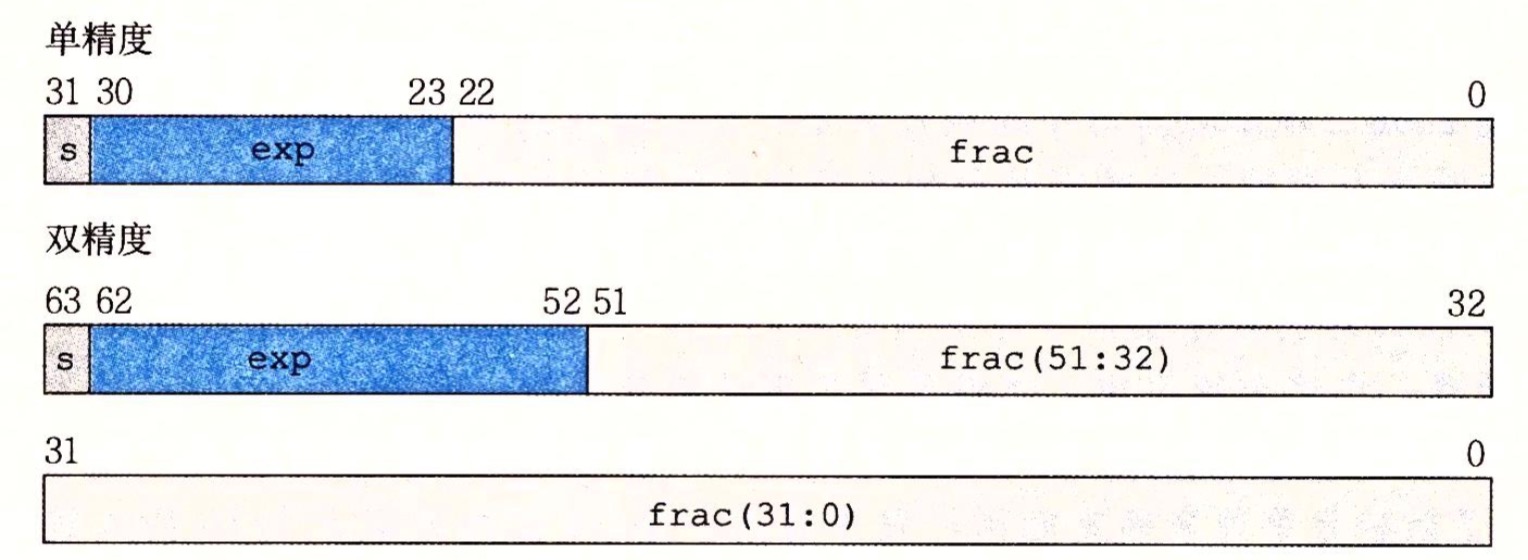
M:二进制中M的第一位总是1,所以IEEE 754规定,这个数字可以忽略,在运算的时候再添上。这样对于32位浮点数,就有24位有效数字,64位则有53位。增加了表示范围
E:E 是无符号的,如何表示负数,也就是 2^-n 这种形式? 实际的E表示为 E = e - Baic。其中e是无符号数,Baic=2^(k-1)-1。以32位浮点数为例,e的范围在0255,Baic = 127,E的范围就是-126+127。
阶码(E)的值决定了 这个数是规格化,非规格化或者特殊值。
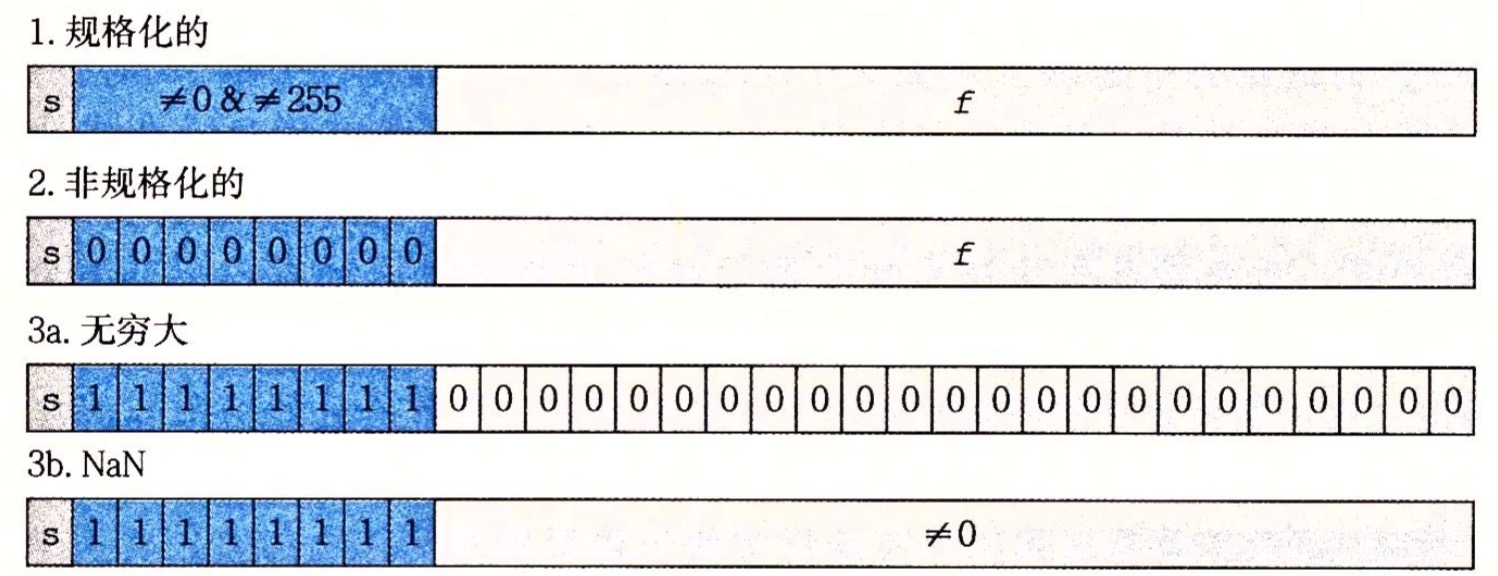
- 规格化:当阶码域不全为0时,或者不全为1时,得到真实值,再将有效数字M前加上第一位的1
- 非规格化:阶码域全为0,小数域不再补上1,这样做是为了表示±0,以及接近于0的很小的数字
- 特殊值:当阶码全为1,小数域全为0的时候,根据s的值,表示为 + \infty,- \infty。如果小数域不全为0,则为NaN
大小端
数据在内存中的存储顺序方式有大小端之分。
举例:如果int类型的x 存储在0x100的位置,十六进制表示:0x01234567 ,根据大小端有两种不同存储方式:
- 大端: 按照最高有效位(这里是01)到最低有效位的顺序存储
| 0x100 | 0x200 | 0x300 | 0x400 |
|---|---|---|---|
| 01 | 23 | 45 | 67 |
- 小端:按照最低有效位(这里是67)到最高有效位的顺序存储
| 0x100 | 0x200 | 0x300 | 0x400 |
|---|---|---|---|
| 67 | 45 | 23 | 01 |
一般在应用层开发无需在意大小端,字节顺序不可见。只有在网络传输的时候,大端机器传输给小端机器,或者反过来时,才会有大小端转换问题。
总结
计算机内存有限,溢出是必须考虑的事情。整数用补码形式存放于计算机,便于进行数值计算。两个数进行计算,当超出类型的字节范围,就会有溢出问题,造成程序异常。一个数据的存放在内存的顺序有大小端之分。
参考
痛苦分两种,一种毫无意义,一种让人更坚强。 – 《纸牌屋》